No world model, no general AI

From Ilya's prediction to Google DeepMind's proof.

Imagine if we could build an AI that thinks and plans like a human. Recent breakthroughs in large language models (LLMs) have brought us closer to this goal. As these models grow larger and trained on more data, they develop the so-called emergent abilities that significantly improve their performance on a wide range of downstream tasks. This has sparked a new wave of research into creating general AI agents that can tackle complex, long-horizon tasks in the real world environments. But here is the fascinating part: humans do not just react to what they see, we build rich mental models of how the world works. These world models help us set ambitious goals and make thoughtful plans. Hence, based on this observation, it is natural to ask:

“Is learning a world model useful to achieve a human-level AI?”

Recently, researchers at Google DeepMind showed that learning a world model is not only beneficial, but also necessary for general agents. In this post, we will discuss the key findings from the paper and the implications for the future of AI agents.

Do we need a world model?

In 1991, Rodney Brooks made a famous claim that “the world is its own best model”.

Figure 1. In Intelligence without representation, Rodney Brooks famously proposed that “the world is its own best model”.

He argued that intelligent behavior could emerge naturally from model-free agents simply by interacting with their environment through a cycle of actions and perceptions, without needing to build explicit representations of how the world works. Brooks’ argument has been strongly supported by the remarkable success of model-free agents, which have demonstrated impressive generalization capabilities across diverse tasks and environments. This model-free approach offers an appealing path to creating general AI agents while avoiding the complexities of learning explicit world models. However, recent works suggest an intriguing possibility: even these supposedly model-free agents might be learning implicit world models and planning algorithms beneath the surface.

Ilya was right all along?

Looking back to March 2023, Ilya Sutskever made a profound claim that large neural networks are doing far more than just next-word prediction and are actually learning “world models”. The way he put it,

In March 2023, @ilyasut made a profound claim about LLMs learning "world models". Now, researchers at @GoogleDeepMind have proven he glimpsed something even deeper; a fundamental law governing ALL intelligent agents. 🧵 pic.twitter.com/MsMx8snUZs

— ohqay (@ohqayy) June 5, 2025

He believed that what neural networks learn are not just textual information, but rather a compressed representation of our world. Thus, the more accurately we can predict the next word, the higher fidelity of the world model we can achieve.

Agents and world models

While Ilya’s claim was intriguing, it was not clear how to formalize it at that time. But now, researchers at Google DeepMind have proven that what Ilya said is not just a hypothesis, but a fundamental law governing all general agents. In the paper, the authors showed that,

“Any agent capable of generalizing to a broad range of simple goal-directed tasks must have learned a predictive model capable of simulating its environment, and this model can always be recovered from the agent.”

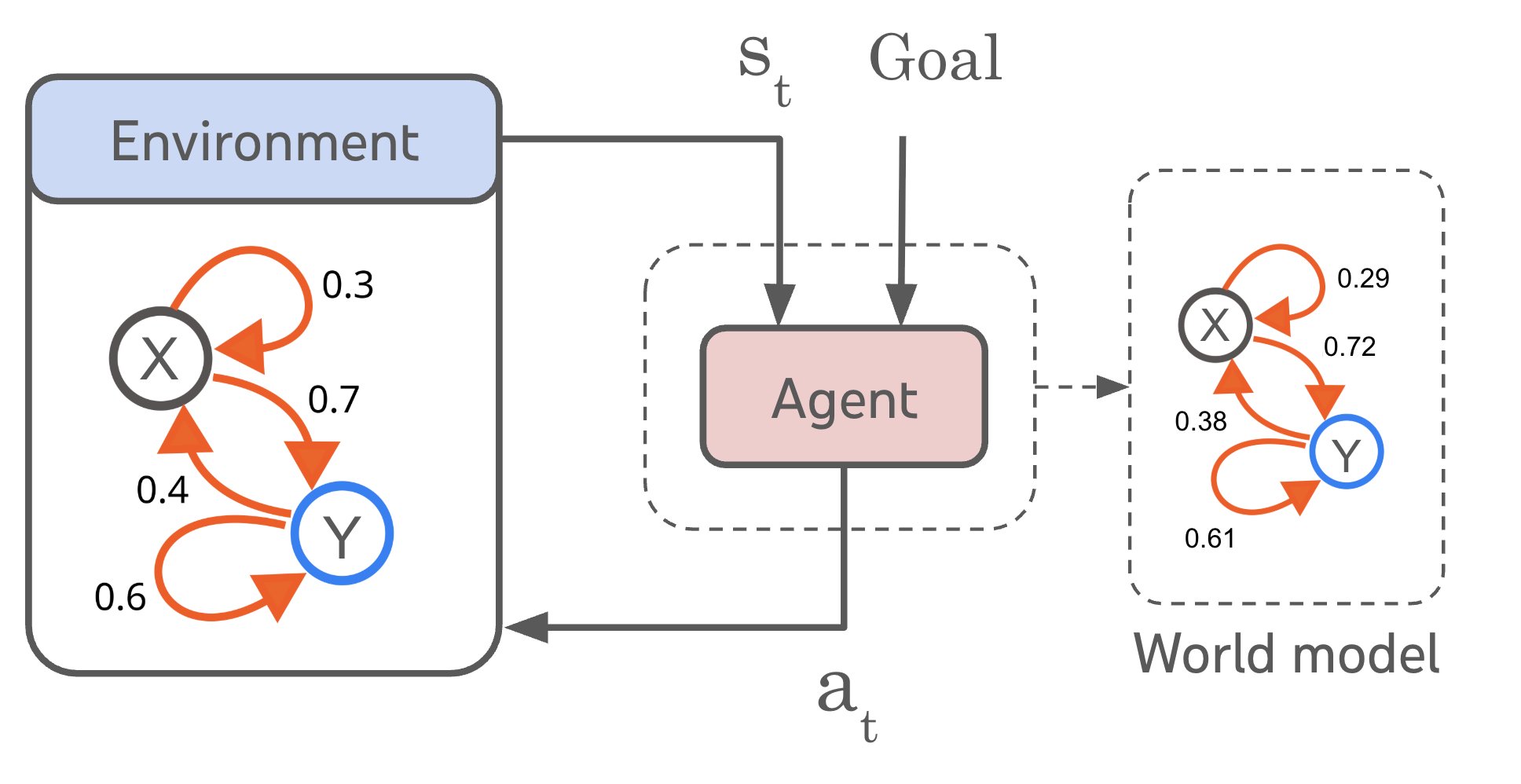
Figure 2. Any agent satisfying a regret bound must have learned an environment transition function, which can be extracted from its goal-conditional policy. This holds true for agents that can handle basic tasks like reaching specific states.

1. There is no “model-free shortcut” to building general AI agents. If we want agents that generalize to diverse tasks, we cannot avoid learning world models.
2. Better performance requires better world models. The only path to lower regret or handling more complex goals is through learning increasingly accurate world models.

The above only holds true for agents that plan over multi-step horizons, as they need to understand how actions affect future states. However, “myopic” agents that only consider immediate rewards can potentially avoid learning world models since they do not need to predict long-term consequences.

To make the above claims more precise, the authors develop a rigorous mathematical framework built on 4 key components: environments, goals, agents, and world models.

Environments

The environment is assumed to be a controlled Markov process (cMP), which is essentially a Markov decision process without a specified reward function. A cMP consists of a state space \(\boldsymbol{S}\), an action space \(\boldsymbol{A}\), and a transition function \(P_{ss'}(a) = P(S_{t+1} = s' \mid A_t = a, S_t = s)\). The authors assume the environment is irreducibleA Markov process is irreducible if every state is reachable from every other state. and stationaryA Markov process is stationary if the transition probabilities do not change over time..

Goals

Rather than defining complex goal structures, the paper focused on simple, intuitive goals expressed in Linear Temporal Logic (LTL). A goal \(\varphi\) has the form \(\varphi = \mathcal{O}([(s,a) \in \boldsymbol{g}])\) where \(\boldsymbol{g}\) is a set of goal states and \(\mathcal{O} \in \{\bigcirc, \diamond, \top\}\) specifies the time horizon (\(\bigcirc\) = next, \(\diamond\) = eventually, \(\top\) = now). More complex composite goals \(\psi\) can be formed by combining sequential goals in ordered sequences: \(\psi = \langle\varphi_1, \varphi_2, \ldots, \varphi_n\rangle\) where the agent must achieve each sub-goal in order. The depth of a goal as the number of sub-goals: \(\text{depth}(\psi) = n\).

Agents

The authors focused on goal-conditioned agents, which are defined as a policy \(\pi(a_t \mid h_t; \psi)\) that maps a history \(h_t\) to an action \(a_t\) conditioned on a goal \(\psi\). This leads to a natural definition of an optimal goal-conditioned agent for a given environment and set of goals \(\boldsymbol{\Psi}\), which is a policy that maximizes the probability that \(\psi\) is achieved, for all \(\psi \in \boldsymbol{\Psi}\). However, real agents are rarely optimal, especially when operating in complex environments and for tasks that require coordinating many sub-goals over long time horizons. Instead of requiring perfect optimality, the authors define a bounded agent that is capable of achieving goals of some maximum goal depth with a failure rate that is bounded relative to the optimal agent. A bounded goal-conditioned agent \(\pi(a_t \mid h_t; \psi)\) satisfies:

\[P(\tau \models \psi \mid \pi, s_0) \geq \max_{\pi'} P(\tau \models \psi \mid \pi', s_0)(1-\delta)\]

for all goals \(\psi \in \boldsymbol{\Psi}_n\), where \(\boldsymbol{\Psi}_n\) is the set of all composite goals with depth at most \(n\) and \(\delta \in [0,1]\) is the failure rate parameter.

World Models

The authors considered the predictive world models, which can be used by agents to plan. They defined a world model as any approximation \(\hat{P}_{ss'}(a)\) of the transition function of the environment \(P_{ss'}(a) = P(S_{t+1} = s' \mid A_t = a, S_t = s)\), with bounded error \(\left|\hat{P}_{ss'}(a) - P_{ss'}(a)\right| \leq \varepsilon\). The authors showed that, for any such bounded goal-conditioned agent, an approximation of the environment’s transition function (a world model) can be recovered from the agent’s policy alone:

Let \(\pi\) be a goal-conditioned agent with maximum failure rate \(\delta\) for all goals \(\psi \in \boldsymbol{\Psi}_n\) where \(n > 1\). Then \(\pi\) fully determines a model \(\hat{P}_{ss'}(a)\) for the environment transition probabilities with bounded error:

\[\left|\hat{P}_{ss'}(a) - P_{ss'}(a)\right| \leq \sqrt{\frac{2P_{ss'}(a)(1-P_{ss'}(a))}{(n-1)(1-\delta)}}\]

For \(\delta \ll 1\) and \(n \gg 1\), the error scales as \(\mathcal{O}(\delta/\sqrt{n}) + \mathcal{O}(1/n)\).

The above result reveals two crucial insights:

1. As agents become more competent (\(\delta \to 0\)), the recoverable world model becomes more accurate.
2. As agents handle longer-horizon goals (larger \(n\)), they must learn increasingly precise world models.

It also implies that learning a sufficiently general goal-conditioned policy is informationally equivalent to learning an accurate world model.

How to recover the world model?

The authors also derived an algorithm to recover the world model from a bounded agent. The algorithm works by querying the agent with carefully designed composite goals that correspond to “either-or” decisions. For instance, it presents goals like “achieve transition \((s,a) \to s'\) at most \(r\) times out of \(n\) attempts” versus “achieve it more than \(r\) times”. The agent’s choice of action reveals information about which outcome has higher probability, allowing us to estimate \(P_{ss'}(a)\).

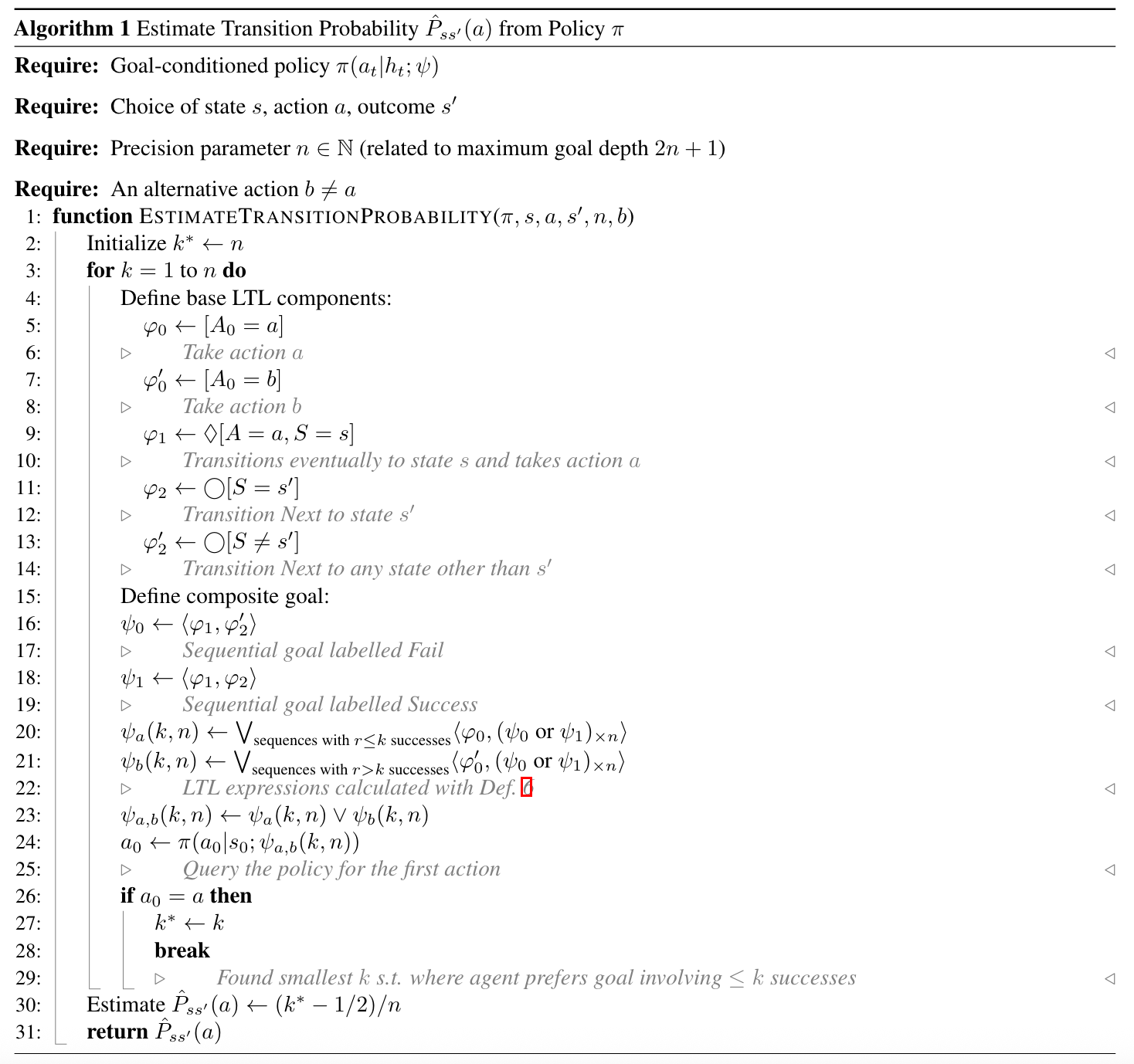
Figure 3. The derived algorithm for recovering a world model from a bounded agent.

Experiments

To test the effectiveness of the algorithm, the authors conducted experiments on a randomly generated controlled Markov process with 20 states and 5 actions, featuring a sparse transition function to make learning more challenging. They trained agents using trajectories sampled from the environment under a random policy, increasing agent competency by extending the training trajectory length (\(N_{\text{samples}}\)). The results show that:

• Even when agents strongly violated the theoretical assumptions (achieving worst-case regret \(\delta = 1\) for some goals), their algorithm still recovered accurate world models.
• The average error in recovered world models decreased as \(\mathcal{O}(n^{-1/2})\), matching the theoretical scaling relationship between error bounds and goal depth.
• As agents learned to handle longer-horizon goals (larger maximum depth \(n\)), the extracted world models became increasingly accurate. This confirms the fundamental link between agent capabilities and world model quality.

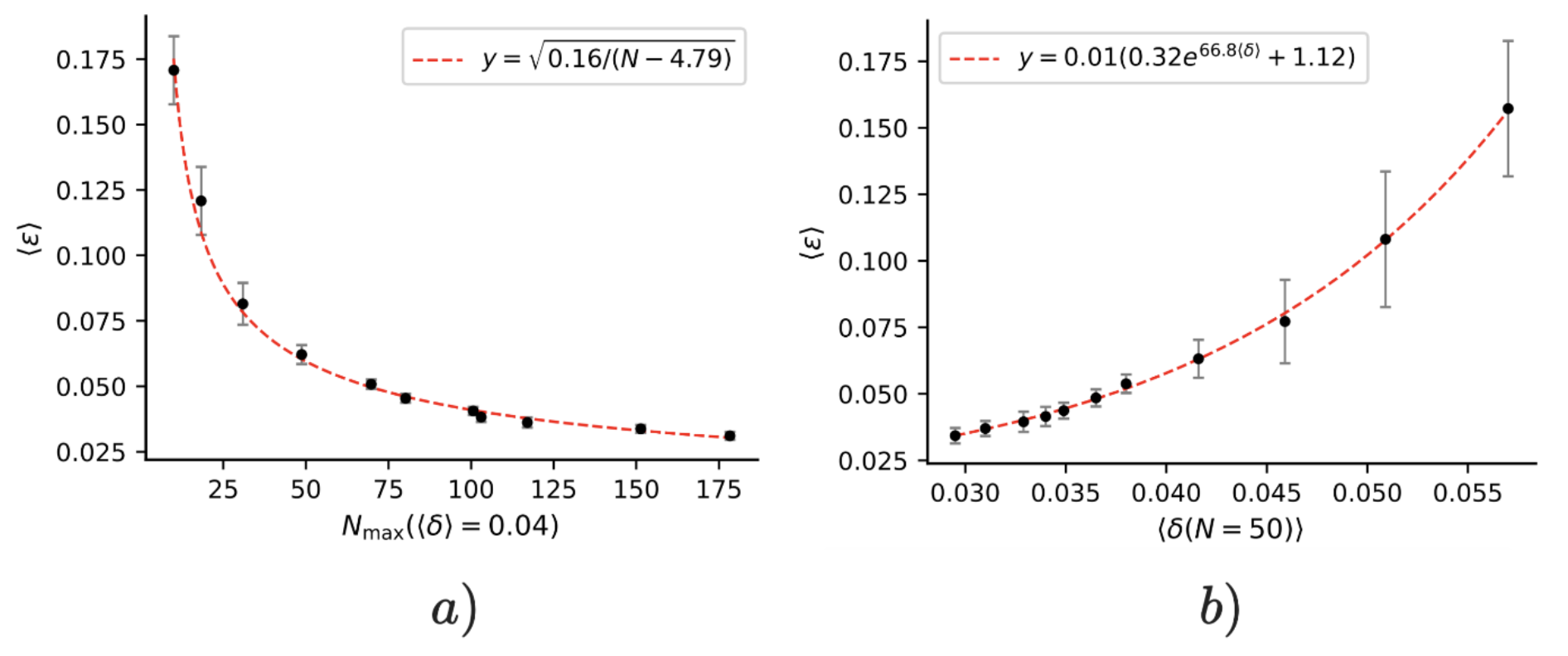
Figure 4. a) Mean error in recovered world model decreases as agent handles deeper goals. b) Mean error scales with agent’s regret at depth 50. Error bars show 95% confidence intervals over 10 experiments.

Connection to related works

The results of this work complement several other areas of AI research:

• The proposed algorithm completes a the “triangle” between environment, goal, and policy. Planning determines an optimal policy given a world model and goal (world model + goal → policy), while inverse reinforcement learning (IRL) recovers goals given a world model and policy (world model + policy → goal). The proposed algorithm fills in the remaining direction by recovering the world model given the agent’s policy and goal (policy + goal → world model). Just as IRL requires observing policies across multiple environments to fully determine goals, the algorithm needs to observe the agent’s behavior across multiple goals to fully recover the world model.

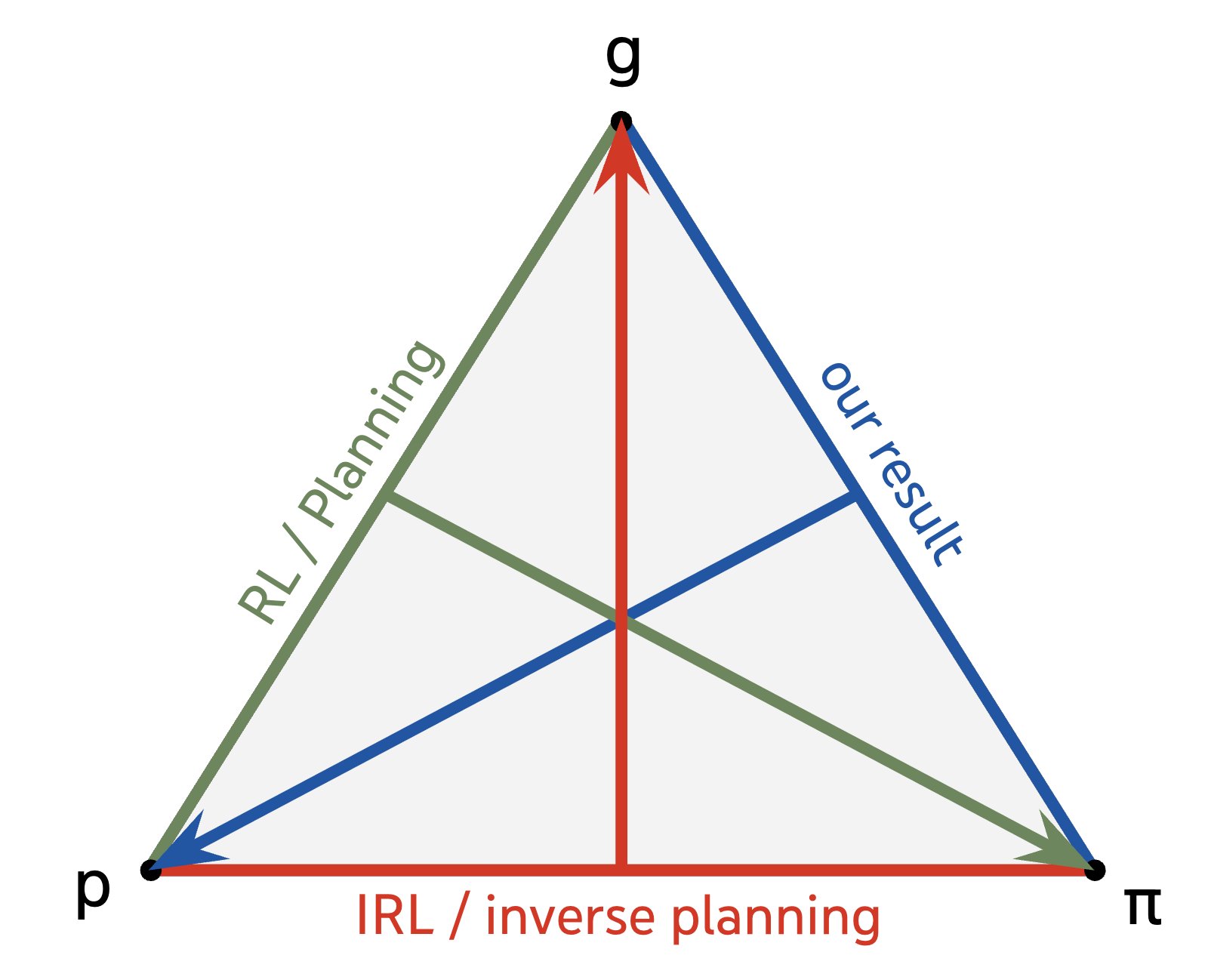
Figure 5. While planning uses a world model and a goal to determine a policy, and IRL and inverse planning use an agent’s policy and a world model to identify its goal, the proposed algorithm uses an agent’s policy and its goal to identify a world model.

• Traditional mechanistic interpretability (MI) typically relies on analyzing neural network activations or using supervised probes, on the other hand, the proposed algorithm provides a novel approach that extracts world models directly from an agent’s policy behavior, making it applicable even when model internals are inaccessible. This unsupervised and architecture-agnostic approach works for any agent that satisfies the bounded regret condition, regardless of its specific implementation. For LLMs, this means we can potentially uncover their implicit world models by analyzing their goal-directed behavior, without needing to access their internal representations.

• A recent work showed that agents adapting to distributional shifts must learn causal world models. This work complements it by focusing on task generalization rather than domain generalization. Interestingly, domain generalization requires deeper causal understanding than task generalization. For example, in a system where state variables \(X\) and \(Y\) are causally related (\(X \to Y\)), an agent can achieve optimal task performance by learning just the transition probabilities, without needing to understand the underlying causal relationship. This suggests an agential version of Pearl’s causal hierarchy, where different agent capabilities (like domain or task generalization) require different levels of causal knowledge.

The findings also have significant implications for AI development and safety. The emergence of new capabilities in large language models and other AI systems could be explained by implicit world models learned while optimizing for diverse training tasks. The ability to extract world models from capable agents provides a new tool for verification and alignment, as model fidelity scales with agent capability. However, the inherent difficulty of learning accurate world models of complex real-world systems also places fundamental limits on general agent capabilities.

Takeaways

Perhaps Ilya’s 2023 prediction was more prophetic than we realized. If the above results hold true, then the current race toward artificial superintelligence (ASI) through scaling language models might be secretly a race toward building more sophisticated world models. It is also possible that we may be witnessing something even more profound: the transition from what David Silver and Richard Sutton call the “Era of Human Data” to the “Era of Experience”. While current AI systems have achieved remarkable capabilities by imitating human-generated data, Silver and Sutton argue that superhuman intelligence will emerge through agents learning predominantly from their own experience. For example, with recent developments in foundation world models like Genie 2, we can generate endless 3D environments from single images and allow agents to inhabit “streams of experience” in richly grounded environments that adapt and evolve with their capabilities.

Figure 6. Genie 2, a foundation world model capable of generating an endless variety of action-controllable, playable 3D environments for training and evaluating embodied agents. Based on a single prompt image, it can be played by a human or AI agent using keyboard and mouse inputs.

If general agents must learn world models, and superhuman intelligence requires learning from experience rather than human data, then foundation world models like Genie 2 might be the ultimate scaling law for the Era of Experience. Rather than hitting the ceiling of human knowledge, we are entering a phase where the quality of AI agents is fundamentally limited by the fidelity of the worlds they can simulate and explore. The agent that can dream the most accurate dreams, and learn the most from those dreams, might just be the most intelligent.