Richard Cornelius Suwandi

I am a fully-funded PhD student at School of Artificial Intelligence, CUHK-Shenzhen, advised by Prof. Feng Yin and Prof. Tsung-Hui Chang. Prior to my PhD, I obtained my BSc degree in Statistics (with first-class honors) from CUHK-Shenzhen. My current research explores:
- Bayesian optimization for sample-efficient black-box optimization and sequential decision-making
- Gaussian processes for probabilisitic modeling and uncertainty quantification
- Foundation models for open-ended algorithm discovery and generative design in science & engineering
If you are interested in collaborating or discussing research ideas, feel free to reach out via email.
News
Jan 18, 2026
🎉 Our paper titled “Breaking the Curse of Dimensionality in Gaussian Process Training With Zeroth-Order Adaptive Perturbation” has been accepted to ICASSP 2026!
Jan 05, 2026
🎓 Transferred to the School of Artificial Intelligence, CUHK-Shenzhen with a fully-funded PhD scholarship!
Dec 01, 2025
🛫 Flew to San Diego for NeurIPS 2025! If you are also attending, feel free to reach out to chat or grab a coffee
Nov 17, 2025
🏆 Selected as the recipient of the Guangdong Government Outstanding International Student Scholarship
Oct 09, 2025
✨ Invited to serve as a reviewer for ICASSP 2026!
Sep 24, 2025
✨ Invited to serve as a reviewer for ICLR 2026!
Sep 19, 2025
🎉 Our paper titled “Adaptive Kernel Design for Bayesian Optimization Is a Piece of CAKE with LLMs” has been accepted to NeurIPS 2025!
Sep 15, 2025
💻 Joined Dria as a Research Intern to work on evolutionary coding agents!
Jul 20, 2025
🏆 Won the 2nd prize award at the 2025 Doctoral Research and AI Innovation Conference held by CUHK-Shenzhen!
May 09, 2025
📚 Our latest work on grid spectral mixture product (GSMP) kernel has been featured in the “Machine Learning: From the Classics to Deep Networks, Transformers and Diffusion Models” book!
Jan 28, 2025
🎉 Our paper titled “Sparsity-Aware Distributed Learning for Gaussian Processes with Linear Multiple Kernel” has been accepted to IEEE TNNLS!
Sep 30, 2024
🏆 Selected as the recipient of the IEEE Signal Processing Society Scholarship!
Sep 10, 2024
📝 My blog post on “Optimize Your Signal Processing with Bayesian Optimization” has been published on IEEE SPS!
Sep 09, 2024
✨ Invited to serve as a reviewer for ICLR 2025!
Jul 17, 2024
🏆 Selected as the recipient of the Shenzhen Universiade International Scholarship Foundation Program!
Aug 14, 2023
🎓 Joined Bayesian Learning for Signal Processing Group as a PhD student!
May 04, 2022
🎉 Our paper titled “Gaussian Process Regression with Grid Spectral Mixture Kernel: Distributed Learning for Multidimensional Data” has been accepted to FUSION 2022!
Jan 30, 2021
🎉 Our paper titled “Demystifying Model Averaging for Communication-Efficient Federated Matrix Factorization” has been accepted to ICASSP 2021!
Selected Works
- 2026
Breaking the Curse of Dimensionality in Gaussian Process Training With Zeroth-Order Adaptive Perturbation
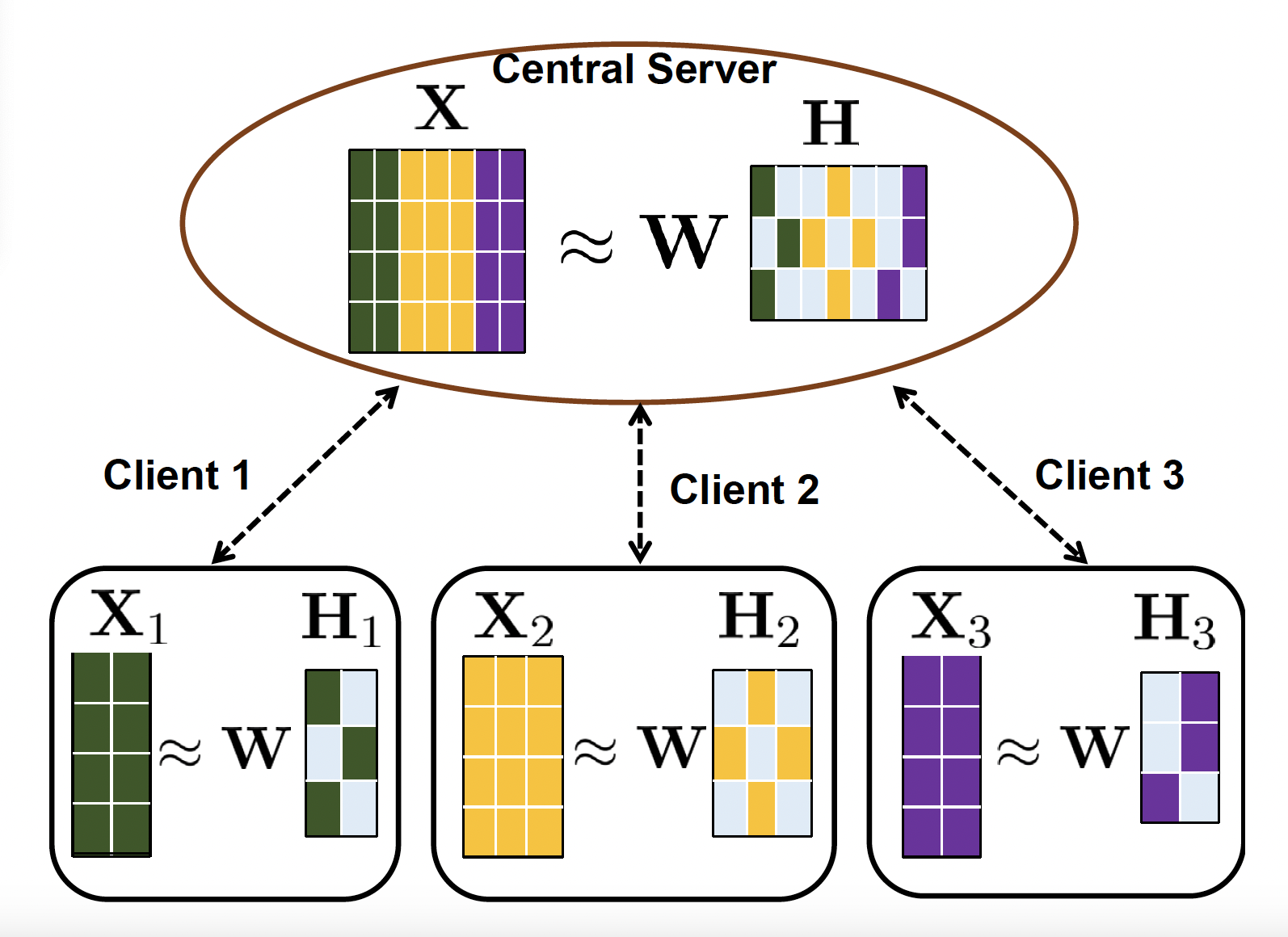
51th IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2026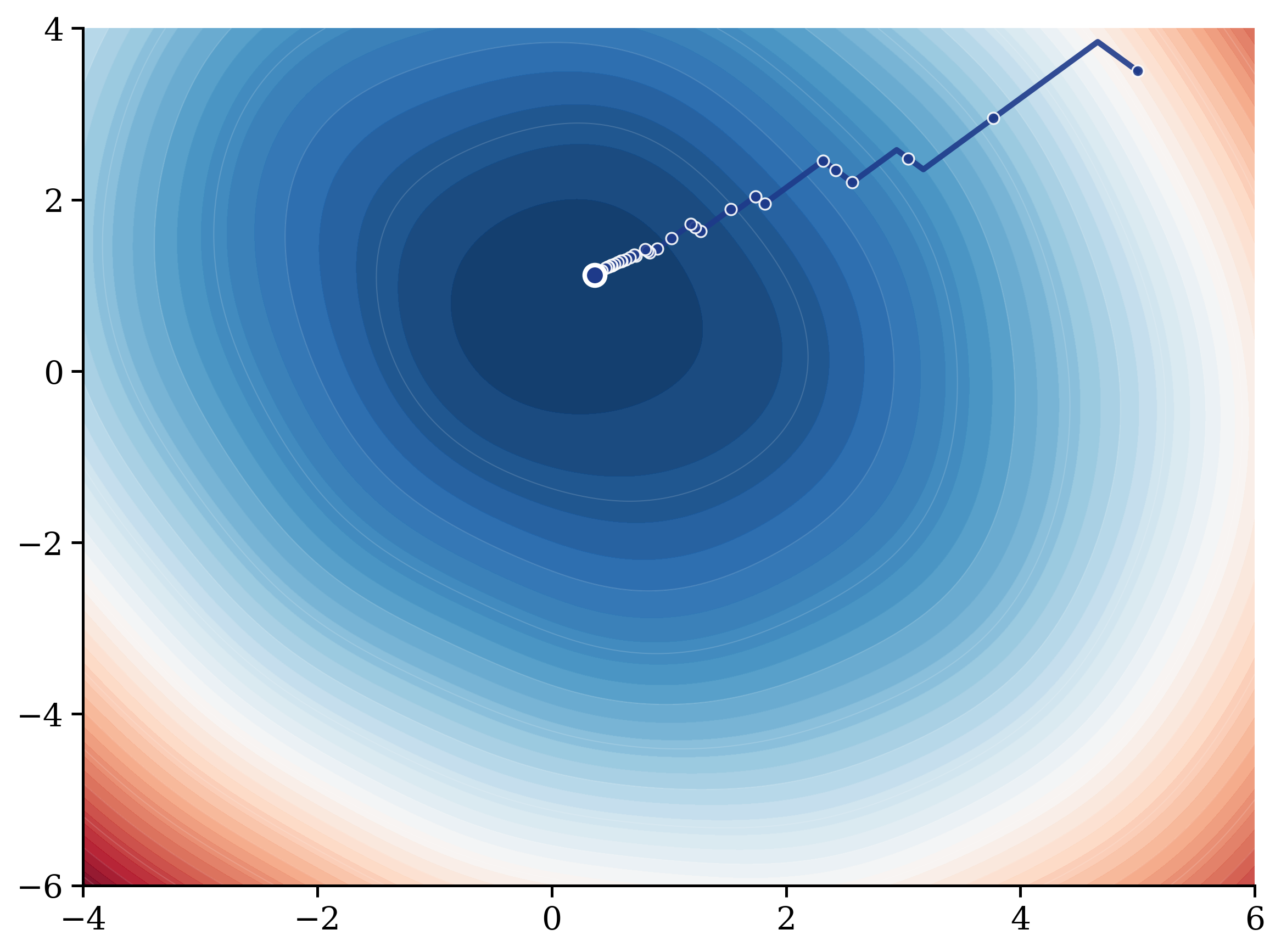
- 2025
Adaptive Kernel Design for Bayesian Optimization Is a Piece of CAKE with LLMs
39th Conference on Neural Information Processing Systems (NeurIPS), 2025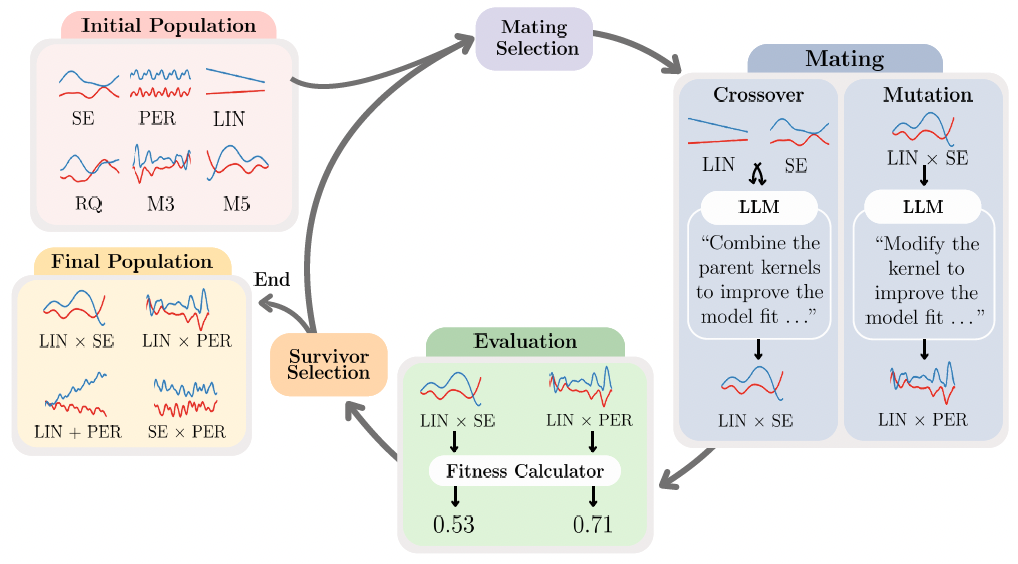
- 2025
Sparsity-Aware Distributed Learning for Gaussian Processes with Linear Multiple Kernel
IEEE Transactions on Neural Networks and Learning Systems, 2025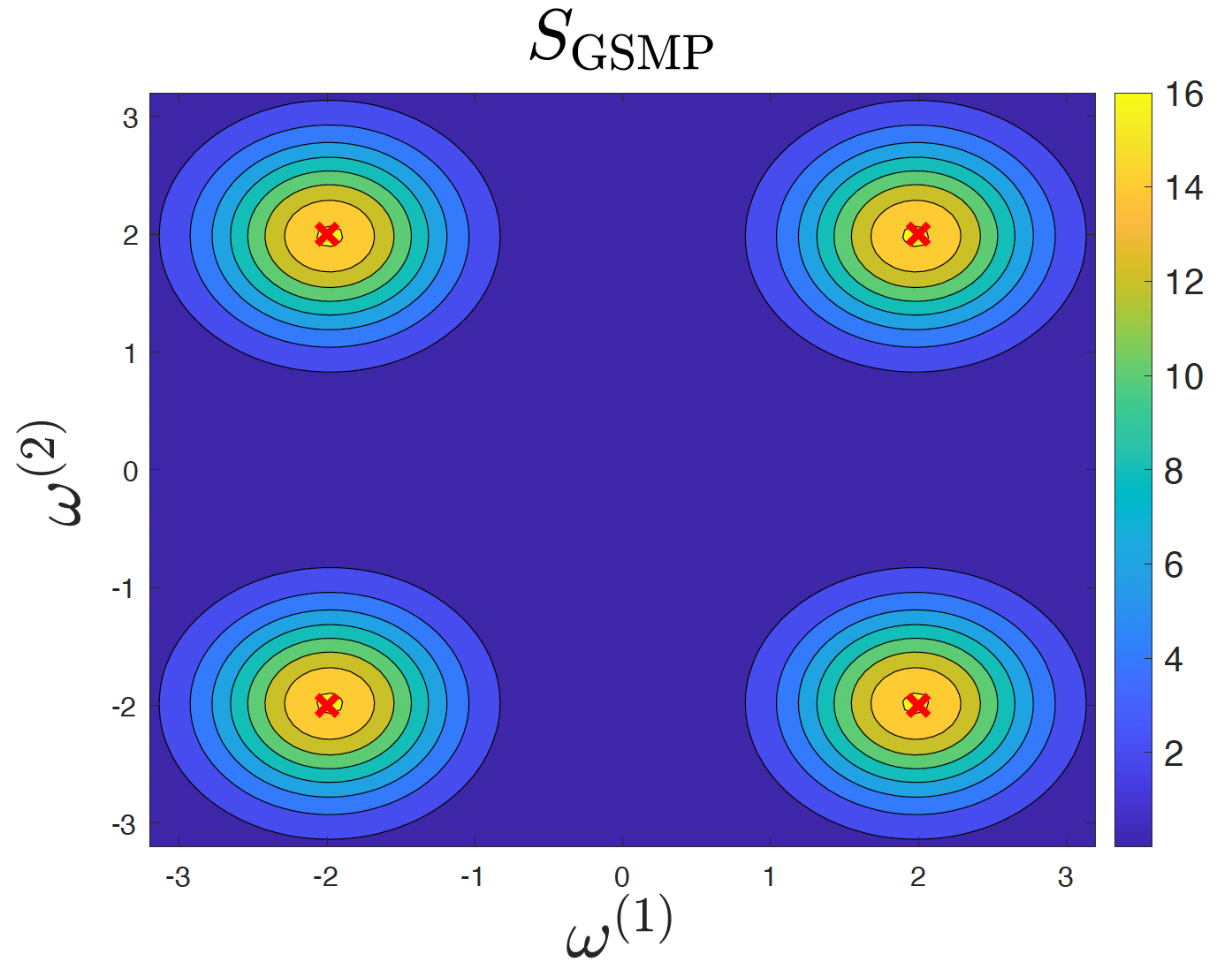
- 2022
Gaussian process regression with grid spectral mixture kernel: Distributed learning for multidimensional data
25th International Conference on Information Fusion (FUSION), 2022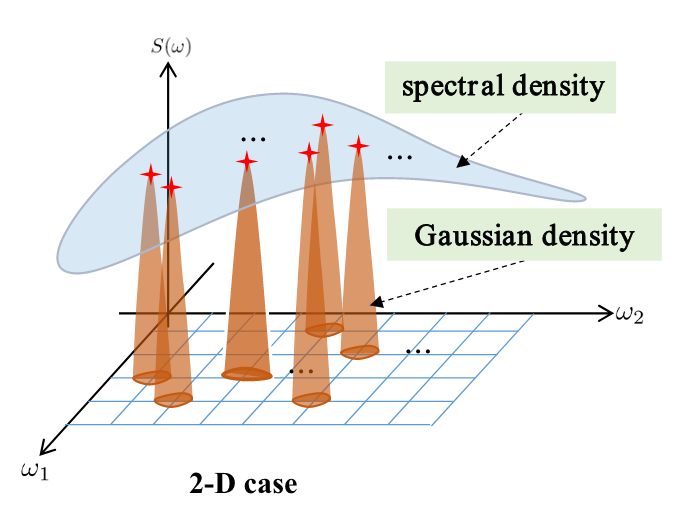
- 2021
Demystifying model averaging for communication-efficient federated matrix factorization
46th IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2021